About branch orders

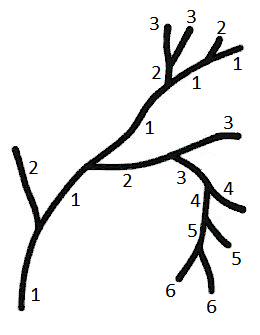
The centrifugal method is the basic scheme to assign branch order to a tree.

• The segment that begins at the origin of the dendrite is assigned the branch order 1.
• The branches that connect to that segment are assigned the branch order 2.
• The branches that connect to those branches are assigned the branch order 3.

This process continues until all branches are assigned a value.

Centrifugal ordering counts the distance from the root in terms of the number of segments traversed. The advantage to centrifugal ordering is that missing portions of the tree do not result in incorrect numbering of the known segments.

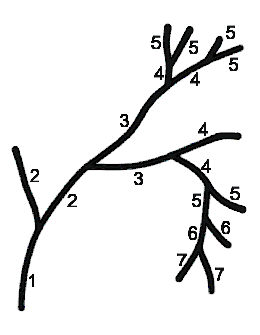
The centripetal method starts with 1 at each terminal segment, and proceeds towards the root.

• Each time a bifurcation node is encountered, the order of the bifurcation becomes the largest order of its two offspring branches, plus one.
• Then the whole parent branch, with its attached markers, is labeled as the bifurcation.

This continues until the segment attached to the root is reached.

The order of a branch is the topological distance (number of nodes to cross) downwards to the farthest terminal branch.

Therefore, the order of the root branch is the depth of the tree minus 1.

The maximum centripetal order "+1" is the same as the maximum centrifugal ordering of the tree.

The centripetal ordering is similar to retrograde maximal ordering; it is referred to as diameter order or Horsfield order in the literature.

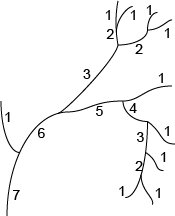
The Strahler method also begins the numbering scheme by assigning the order "1" to all of the terminal segments

• Order assignment progresses towards the root segment.
• At each node, if all offspring segments are assigned the same order, the parent segment is assigned the offspring segments order "+1."
• If the offspring segments are assigned different orders, the largest order is assigned to the parent segment.

The Strahler ordering method increases the order if the offspring segments are balanced trees.

If the offspring segments are not balanced, however, it is the part of the tree that had the most balance that is used as the order number. Unlike the previous ordering schemes, Strahler ordering does not use a topological distance property.

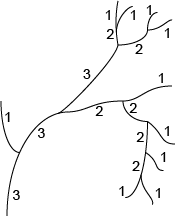
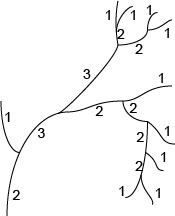
The terminal distance ordering begins at the terminal segments and works towards the root.

• Each terminal segment is assigned an order of "1."
• The parent segments are assigned an order "+1" than the smallest of the orders of the offspring segments; the relationship with the other offspring segments is not known.

The order of a segment is the topological distance (number of nodes to cross) downwards to the closest terminal branch. Therefore the order of the root segment is the minimal depth of the tree. This contrasts with the centripetal ordering that is the maximum distance.

The terminal distance ordering is similar to retrograde minimal ordering.

Microvascular branch ordering is based on vessel diameter and branching order.

In general, when a parent vessel splits:

• the offspring branch with the larger diameter and smaller branching angle retains the same branch order
• the smaller branch with the greater angle is assigned the next successive branch order (similar to the Shaft ordering method).

The specific rules and exceptions are as follows:

1. If the offspring vessel branches at an angle greater than 20º from the projected axis of the parent vessel, it is assigned the next higher branch order (e.g., 1A, 2A, 3A, etc. for arteriolar branches).
2. If both offspring vessels diverge at less than 20º from the parent, the one that diverged at a smaller angle will retain the parent's branch order and the other will receive the next higher order.
3. If both offspring vessels diverge at the same angle, both will receive the successive branch order.
4. If there is greater than 20% change in the diameter of the vessels at a branch point, then the next branch order is assigned; this takes precedence so that if both offspring vessels diverge at less than 20° (see #2) but both decrease diameter by more than 20%, both are assigned the next branch order.

Shaft order is only displayed in Neurolucida Explorer if it has been previously assigned in Neurolucida.

• The shaft order method assigns a path from the root of the tree to a designated primary ending as order "1."
• All segments attached to the main path are assigned order "2."
• The default centrifugal ordering is used to assign orders to all of the remaining segments.

Shaft ordering recognizes that the tree is dominated by one main path and that all other portions of the tree are subsidiary to the main path. The main path can be changed, resulting in a re-numbering of the tree.

As shown below, all segments along the primary branch are designated with a "1."