Polar histogram

Use to avoid the disconnection problem associated with the traditional histogram (i.e., the right side of the histogram is connected to the left side) and to make the information easier to interpret visually.

Perform for dendrites, axons, and apical dendrites.

Apply to the results of the Fan In transform by checking the Apply Fan-in Transform checkbox.

While it is generated, a polar histogram breaks each segment of a tree into a series of straight line segments.

• These segments are collected in bins according to directional orientation.
• The total length in a given bin is summed as a wedge with the same orientation as the line segments, and represented in the circular polar histogram graph.

The 3D tracing is reduced to a 2D polar histogram, that is, the spatial geometry is transformed into length and direction. The polar histogram considers direction to be a local property of the process (while the wedge analysis describes direction relative to a fixed point for all of the dendritic processes).

The right side of a circle has a tangent that runs vertically.

• If the circle is drawn clockwise, then the tangent points down; the angle is 270 degrees.
• Move along the circle to the bottom of the circle and the tangent now points to the left; the angle is 180 degrees.
• Continue further around the circle and the tangent now points up; the angle is 90 degrees.
• Continue on to the top of the circle and the tangent now points to the right; the angle is 0 degrees.

Throughout this circumnavigation of the circle, all directions are equally represented. A polar histogram of a circle is a solid circle around the center of the graph.

Although projection collapses Z, length in Z is used in the length calculation for the polar histogram. The total length in the polar histogram is the same as the total length of all processes used in the polar histogram analysis.

Analysis can be performed for dendrites, axons, and apical dendrites. The polar histogram can also be applied to the results of the Fan-In transform by checking the Apply Fan-in Transform box.

1. Open a data file.
2. Select Analyze>Neuron data>Orientation and open the Polar Histogram Analysis window.
3. Select the branched structures you wish to analyze.

   Click Select All to select all structures, or click Select None to clear these check boxes.

4. Select Apply Fan-in Transform to have this method applied to the data.
5. Click Display. Neurolucida Explorer displays a Polar Histogram window for each type of structure .

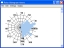The instructions below refer to the Polar Histogram menu (not the general Neurolucida Explorer menu).

Printing a Polar Histogram

• Select File>Print.

Copying a graph or histogram data

• Select Edit>Copy Graph to Clipboard/Copy Histogram Data to Clipboard.
• From the Clipboard, paste the graph or histogram data into another program such as Microsoft Word or Microsoft Excel.

Changing settings

1. Select Settings.
2. Type a number of intervals between 2 and 120 in the number of intervals in histogram field.
   • The number of intervals determines the number of bins.
3. Select Use cubic spline smoothing to minimize the effects of artifacts from the data collection process (especially if fine continuous tracing was used).

More on cubic splines

The discrete coordinates of the computer are similar to a checkerboard.

• A square on a checkerboard has 8 neighbors and therefore only 8 available directions.
• A polar histogram reveals this artifact by having prominent wedges at the 8 principle directions of 0, 45, 90, 135, 180, 225, 270, and 315 degrees.
• The tracing can be smoothed to remove the 8-neighbor artifact. Cubic splines are used for the smoothing process because they are the simplest form of curve that is capable of representing 3-dimensional curves of the type present in the tracing.

Example

The example illustrates the difference that cubic spline smoothing makes in the analysis of the data.

This tracing was analyzed without (left) and with (right) cubic spline smoothing.

• The histogram on the left (without) has prominent wedges at 0, 45, and 90 degrees. These 3 directions are the neighbors used to draw a line that trends up, right, and diagonally up and right.
• The histogram on the right (with) shows a more accurate representation of the directional growth of the line.
  
  

4. Select Choose Color to change the color of the histogram.

Changing the display options

Radial Length—Adds or removes radial length markers from the display.

Degree Ticks—Adds or removes degree ticks from the display.

Outline Pie Segments—Adds or remove a black outline around the pie segments.